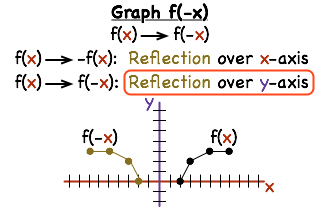
[最も人気のある！] reflection graph y =- f x 279654-Reflection graph y axis

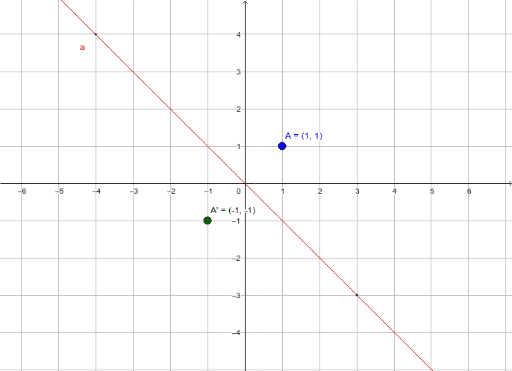
 For example, when point P with coordinates (5,4) is reflecting across the Y axis and mapped onto point P', the coordinates of P' are (5,4)Notice that the ycoordinate for both points did not change, but the value of the xcoordinate changed from 5 to 5 You can think of reflections as a flip over a designated line of reflectionFree graphing calculator instantly graphs your math problemsA Reflect the graph f(x) = V« in the xaxis, then translate it 6 units to the left b Reflect the graph f(x) = \x in the yaxis, then translate it 6 units to the right c Reflect the graph f(x)= x in the yaxis, then translate it 6 units to the left d Question 8 Which of the following transformations is required to graph y= x 6 from

Learn About Reflection Over The Line Y X Caddell Prep Online

Reflection graph y axis

Reflection graph y axis-In this video, you will learn how to do a reflection over the line y = x The line y=x, when graphed on a graphing calculator, would appear as a straight line cutting through the origin with a slope of 1 For triangle ABC with coordinate points A (3,3), B (2,1), and CThe reflections of graphs in the x and y axes are explored by comparing the graphs of f (x), f (x), f (x) and f (x) f (x) ( blue ) , f (x) ( green ), f ( x) ( red ) and f ( x) ( magenta ) The function f (x) is a quadratic function of the form f (x) = ax 2 bx c The exploration is carried out by changing the parameters a, b

Reflecting Compressing Functions Video Khan Academy

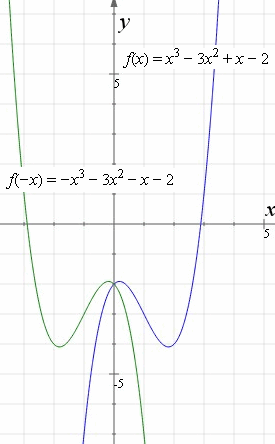
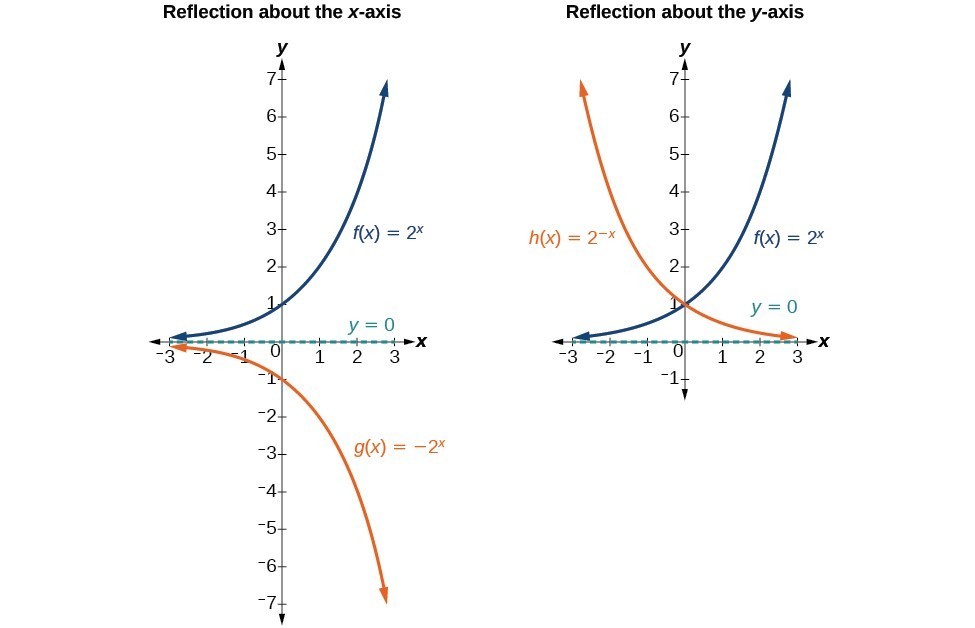
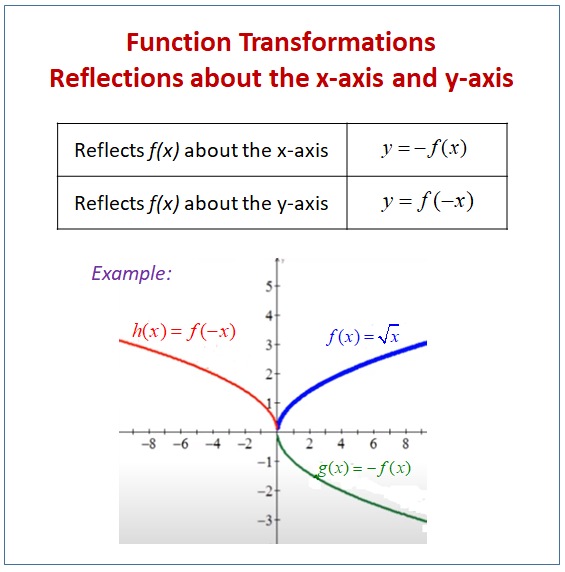
The graph of \ (h (x) = \dfrac {1} {2}\abs {x}\) is a vertical compression of the basic graph \ (y = \abs {x}\) by a factor of \ (2\text {,}\) combined with a reflection about the \ (x\)axis You may find it helpful to graph the function in two steps, as shown in Figure263 Figure 263 Example264 y=f(x) will indicate that the graph has reflected about the origin If I have f(x)=(x) 3 , then the graph would be reflected about the yaxis Try to experiment on these transformations by using a graphing utility such as Desmos , Symbolab , GeoGebraIf we know the graph of y = f (x), we can obtain the graph of its reflection in the xaxis by multiplying the ycoordinate of each point on the graph of y = f (x) by –1 This would give the graph of y = – f (x) Similarly, the value of y = f (–x) at x is the same as the

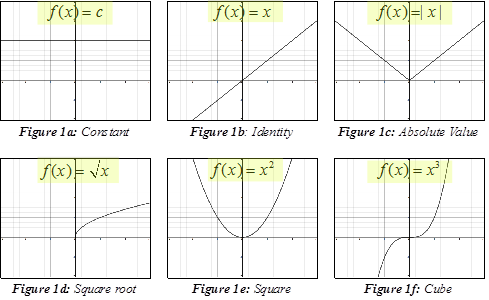
Let us start with a function, in this case it is f(x) = x 2, but it could be anything f(x) = x 2 Here are some simple things we can do to move or scale it on the graph We can move it up or down by adding a constant to the yvalue g(x) = x 2 C Note to move the line down, we use a negative value for C C > 0 moves it up;PUSHING THE XREFLECTION BUTTON FLIPS FUNCTIONS ABOUT THE YAXIS y = f(– x) Do you see how the negative sign is on the inside of the function affecting the xvalue of the function?Swap places of x and y around True for any graph ln (x) is a reflection of e^x due to the same procedure 0 reply X start new discussion

Functions of graphs can be transformed to show shifts and reflections Graphic designers and 3D modellers use transformations of graphs to design objects and imagesGraph functions using reflections about the xaxis and the yaxis Another transformation that can be applied to a function is a reflection over the x – or y axis A vertical reflection reflects a graph vertically across the x axis, while a horizontal reflection reflects a graph horizontally across the y Reflections Suppose that an engineer, Bob, has a blueprint containing a graph of the following function f(x) = x 2 2x 3 ;

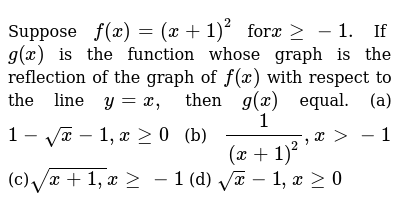
Suppose F X X 1 2 Forxgeq 1 If G X Is The Function Whose Graph Is The Reflection Of The Graph Of F X With Respect To The Line Y X Then G X Equal A 1 Sqrt X 1 Xgeq0 B 1 X 1 2 X Gt 1

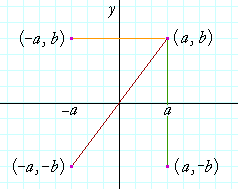
Reflections Of A Graph Topics In Precalculus

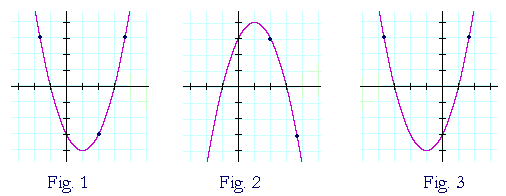
We can reflect the graph of y=f(x) over the xaxis by graphing y=f(x) and over the yaxis by graphing y=f(x) See this in action and understand why it happensIn this series of activities, we will be tying two topics together, transforming a graph that is given both in function notation f(x) and cartesian y = How to transform graphs When studying shapes, you will have become familiar with the four different types of transformation reflection, rotation, translation and enlargementAgain, Fig 1 is y = f(x) Its reflection about the xaxis is y = −f(x) Every yvalue is the negative of the original f(x) Fig 3 is the reflection of Fig 1 about the yaxis Every point that was to the right of the origin gets reflected to the left And every point that was on

Translations Of A Graph Topics In Precalculus

The Function F X 4x The Graph Of G X Is F X Vertically Stretched By A Factor Of 6 And Reflected In The Y Axis What Is The Function Rule Enotes Com

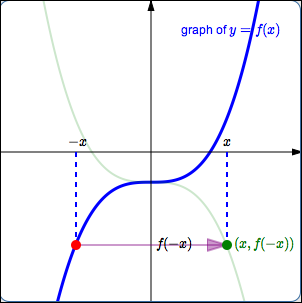
Y = f (x) y = f (−x) Remember, the only step we have to do before plotting the f (x) reflection is simply divide the xcoordinates of easytodetermine points on our graph above by (1) When we say "easytodetermine points" what this refers to is just points for which you know the xLet y = f(x) be a function In the above function, if we want to do reflection through the yaxis, x has to be replaced by x and we get the new function y = f(x) The graph of y = f(x) can be obtained by reflecting the graph of y = f(x) through theWe can also reflect the graph of a function over the xaxis (y = 0), the yaxis(x = 0), or the line y = x Making the output negative reflects the graph over the x axis, or the line y = 0 Here are the graphs of y = f ( x ) and y = f ( x )

Graph Domain And Range Of Absolute Value Functions

How To Reflect A Graph Through The X Axis Studypug

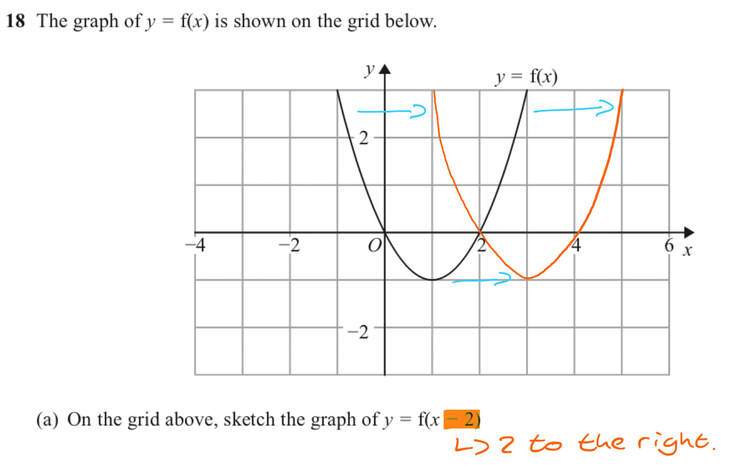
Then the graph of y = f (x c) is obtained by I start with e^x which is a curve that follows y=0 then starts to rise more abruptly at x=0 If f (x) Makes you reflect over the x axis Then e^x will do a neccesary reflection for reflecting it about y = 2 Then I add 2 to the end of f (x) = (e^x)2 = 2e^x Although on my homework they say the correct answer is 4 e^xTutorial on transformations of graphs and more specifically, reflections on the xaxis and yaxisYOUTUBE CHANNEL at https//wwwyoutubecom/ExamSolutionsEXA

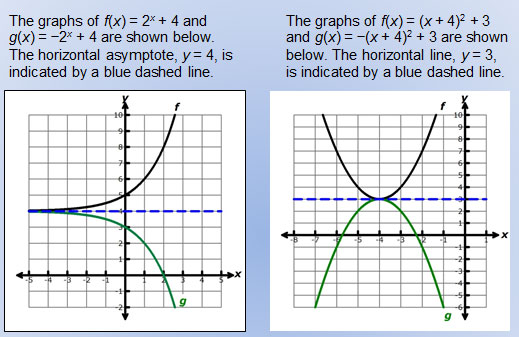
Untitled Document

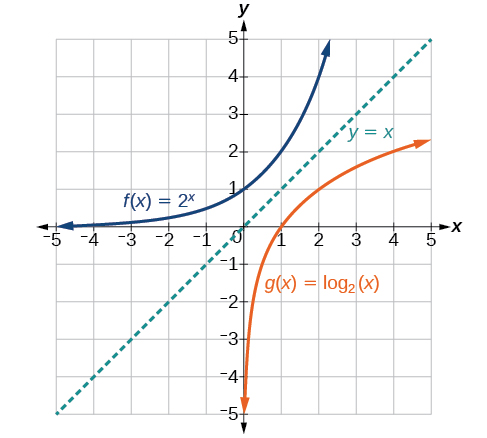
Graphs Of Logarithmic Functions Algebra And Trigonometry

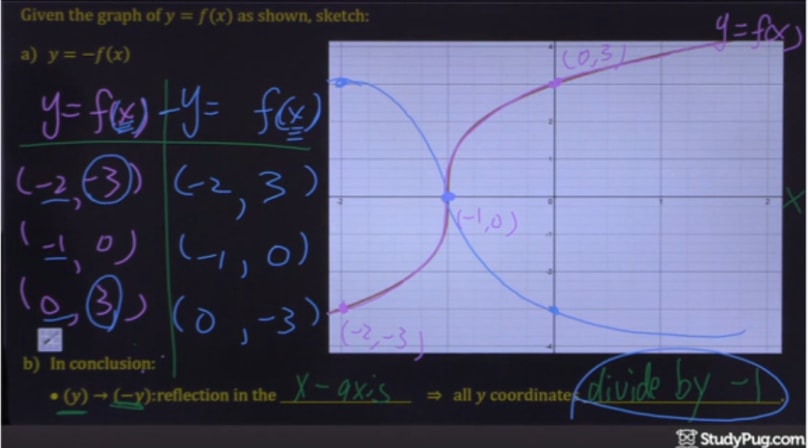
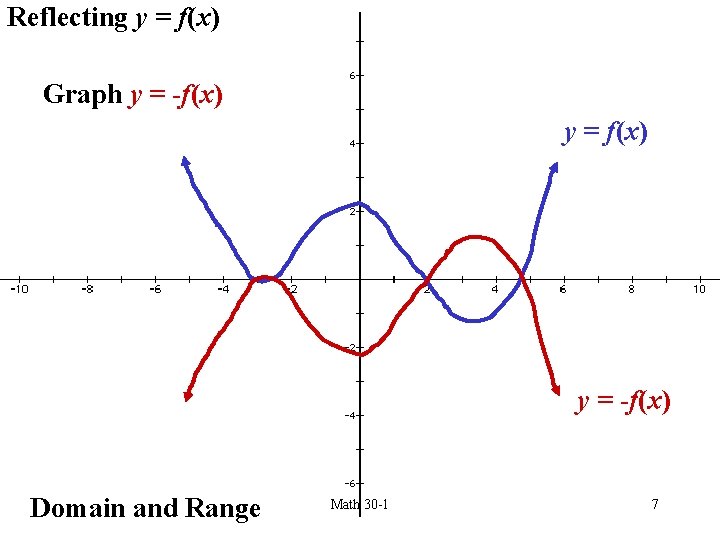
Geometric Transformations of Functions We start with a java applet to explore graphically the basic geometric transformations of functions We now proceed to express these geometrical transformations in algebraic terms Translations of Functions Suppose that y = f (x) is a function and c > 0;The function and itsThe graph of y =−f(x) is a reflection of the graph ofy =f(x) in the xaxis As noted in Example 1, the two graphs have the same xintercepts Points that lie on the xaxis have a ycoordinate of 0, so they are unaltered by the transformation of y =f(x) to y =−f(x) Points that are unaltered by a transformation are said to be invariant –2

Reflecting Graphs

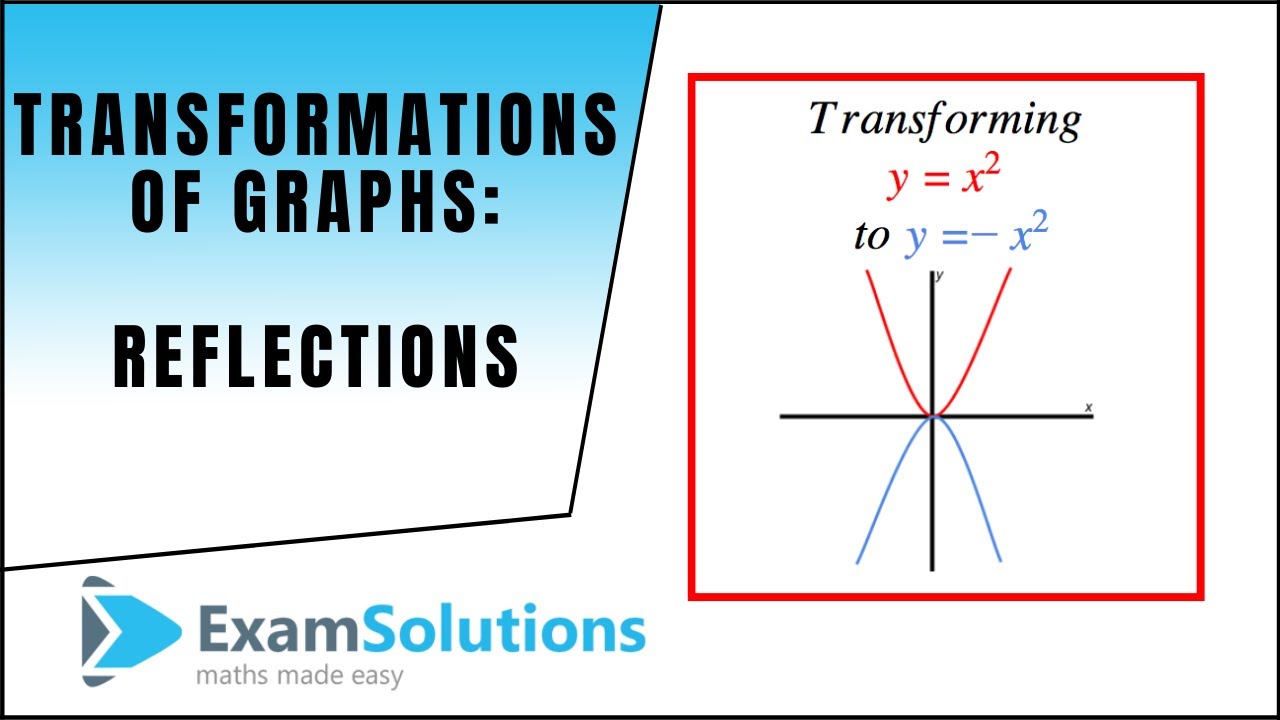
Transformations Of Graphs Reflections Y F X F X Examsolutions Youtube

 Two examples are shown The first is a reflection across the xaxis and the second is a reflection across the yaxisThe rule replacing x by x in the right side of the equation for f(x) results in a reflection of the graph into (or across) the yaxis y = f(x1)1 If the red graph below is of f(x) Then the green graph below is f(x1) 1 Two things were done to f(x) First x was replaced by (x1) which moves the graph LEFT by 1 unitC < 0 moves it down

Solved O Graphs And Functions Transforming The Graph Of A Function By Reflecting Over An Axis A Thi V Hofy F X Is Shown Draw The Graph Of Y Course Hero

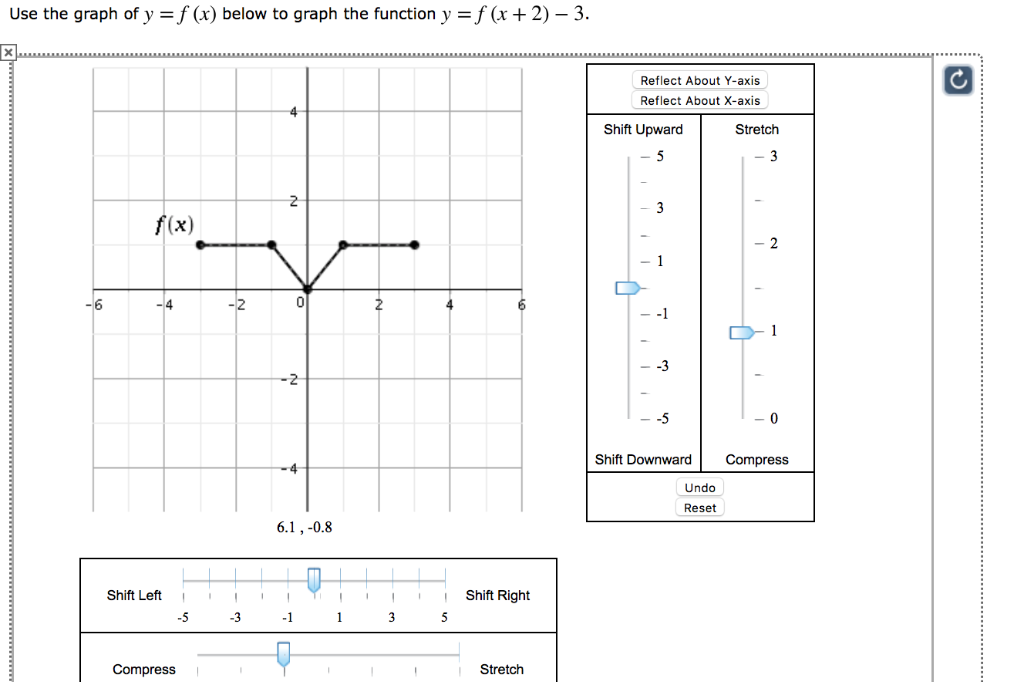
Solved Use The Graph Of Y F X Below To Graph The Function Chegg Com

Y=f(−x) may be obtained by a reflection about the ____ axis of the graph of the function y=f(x) y The graph of a function is the graph of its Ordered Pairs Jus tread and comprehend notecard Assume that f is a function defined on an open interval IIf you reflect a point in the line y=x, your coordinates will simply swap place This is the simple observation you need to make before generalising it This is why in an equation thats all you need to do;Access Card MathZone College Algebra (9th Edition) Edit edition Solutions for Chapter 33 Problem 3E Explain why the graph of y = −f (x) is a reflection of the graph of y = f (x) about the x axis, and why the graph of y = f (−x) is a reflection about the y

Stretching Compressing Or Reflecting A Logarithmic Function College Algebra

Content Geometric Transformations Of Graphs Of Functions

Functions of graphs can be transformed to show shifts and reflections Graphic designers and 3D modellers use transformations of graphs to design objects and imagesThe graph of y = f(x) is the reflection of the graph y = f(x) in the x axis y x y = f(x) y = f(x) Transformation of graphs Rule 1 The graph of y = f(x) is – A free PowerPoint PPT presentation (displayed as a Flash slide show) on PowerShowcom id 3c4477NGY0NAnswer (1 of 14) f(x) means that you replace every 'x' by x f(x) means that you change or of f(x) It is the same function, if the function only has x with odd exponents like x, x^3, x^5, x^(7) etc However, if you have anyhing else, f(x) is not f(x) For example, f(x)= x^2 f(x

Reflecting Compressing Functions Video Khan Academy

Vertical Stretches About An Axis Y Fx The

Reflect in the axis Left 2 f x x g x hx x x y o o Note In part (a), hx can also be written as h x x 2 (b) 2 Left 2 f x x g x h xx x 2 y o o (c) No, parts (a) and (b) do not yield the same function, since z xx22 Both graphs are shown below to emphasize the difference in the final results (but weExample y = – x will flip the function about the yaxis If the negative sign belongs to the xvalue the graph will reflect about the yaxis RememberReflect the graph in the 𝑦 a x i s reflect the graph in the line 𝑦 = 𝑥 reflect the graph in the line 𝑦 = − 𝑥 Q2 Find 𝑔 ( 𝑥), where the graph of the function 𝑔 ( 𝑥) is a reflection across 𝑥 a x i s of the graph of the function 𝑓 ( 𝑥) = 2 𝑥 5 Q3 This is the graph of 𝑦 = 𝑔 ( 𝑥) Which

How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics

Learn About Reflection Over The Line Y X Caddell Prep Online

How To Given a function, reflect the graph both vertically and horizontally Multiply all outputs by –1 for a vertical reflection The new graph is a reflection of the original graph about the x x axis Multiply all inputs by –1 for a horizontal reflection The new graph is a reflection of the original graph about the y y axisOdd Function A function f f is called an odd function if f(x)= −f(−x) f ( x) = − f ( − x) for all x x in the domain of f f In other words, a function is odd if performing a reflection about the y y axis and x x axis (doesn't matter which is performed first) does not change the graph of the function To help remember the definitionF (x) is the graph we are given To go from f (x) to f (x), change the sign of each xvalue in the f (x) function Going from f (x) to f (x) would give us a reflection over the xaxis Going from f (x) to f (x) is what we need to do, and this will be a reflection over the yaxis Figure out how far each point in f (x) is from the yaxis

Q18 Answers Paper 1 November 18 Edexcel Gcse Maths Higher Elevise

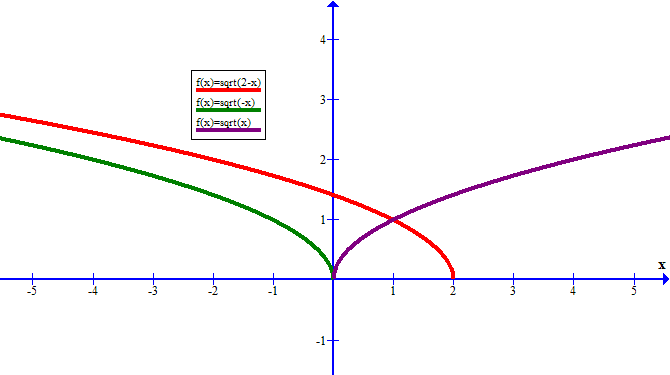
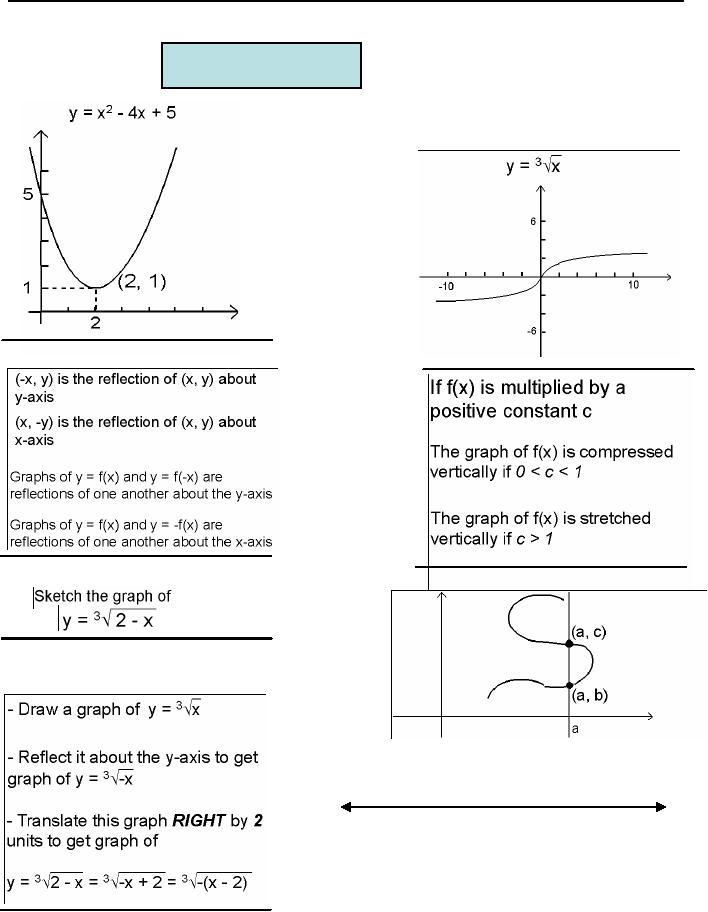
How Do You Graph Y Sqrt 2 X And How Does It Compare To The Parent Function Socratic

A reflection takes whatever graph we have and flips it across either the xaxis or yaxis The graph below has an example of each of these reflections with respect to our parent graph Notice that there are only two graphs In some cases, the reflection acroff one of the axis, just gives back the original equation To see other examples ofGet the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlpha(ii) The graph y = f(−x) is the reflection of the graph of f about the yaxis (iii) The graph of y = f −1 (x) is the reflection of the graph of f in y = x Translation A translation of a graph is a vertical or horizontal shift of the graph that produces congruent graphs The graph of y = f(x c), c > 0 causes the shift to the left y

4 3 Reflecting Graphs

Manipulating Graphs

Find stepbystep Calculus solutions and your answer to the following textbook question Starting with the graph of y=e^x, write the equation of the graph that results from reflecting about the xaxis and then about the yaxisA function may be thought of as a rule which takes each member x of a set and assigns, or maps it to the same value y known at its image x → Function → y A letter such as f, g or h is often used to stand for a functionThe Function which squares a number and adds on a 3, can be written as f(x) = x 2 5The same notion may also be used to show how a function affects particular valuesThe graph of y = f (x) is the graph of y = f (x) reflected about the x axis Here is a picture of the graph of g(x) = (x 2 1) It is obtained from the graph of f(x) = x 2 1 by reflecting it in the xaxis

Reflections Across Y X Geogebra

Transformations Of Functions Mathbitsnotebook A1 Ccss Math

Function Transformations

Solved Suppose The Point 8 12 Is On The Graph Of Y F X Find A Point On The Graph Of The Reflection Of Y F X A Across The X Axis B Across The Y Axis

What Is Difference Between Math X F Y Math And Math Y F X Math Graph Quora

How To Reflect A Graph Through The X Axis Studypug

Graphs Of Functions Calculus And Analytical Geometry Formal Sciences Mathematics

Section 4 3 Reflecting Graphs Symmetry Objective To Reflect Graphs And To Use Symmetry To Sketch Graphs Ppt Download

Solution Suppose The Functions F X And G X Are Inverse Functions About What Line Is The Graph Of G X A Reflection Of The Graph Of F X

Reflecting About Axes And The Absolute Value Transformation

1 5 Shifting Reflecting And Stretching Graphs

Stretching Compressing Or Reflecting An Exponential Function College Algebra

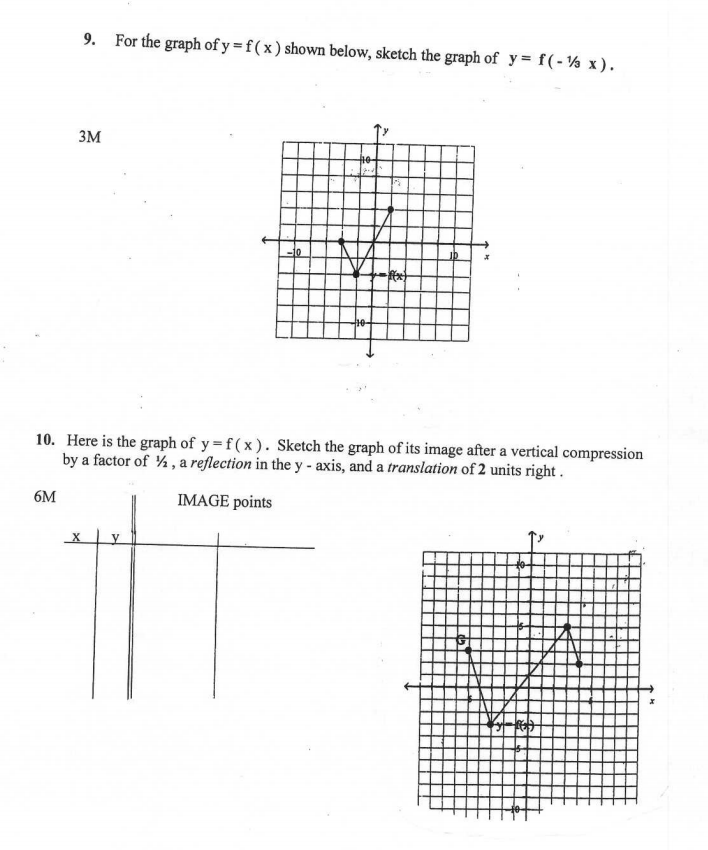
Solved 9 For The Graph Of Y F X Shown Below Sketch The Chegg Com

Reflecting Functions Or Graphs Examples Solutions Worksheets Videos Games Activities

How Do You Graph A Reflection Of A Function Virtual Nerd

Graphing Reflecting Functions Study Com

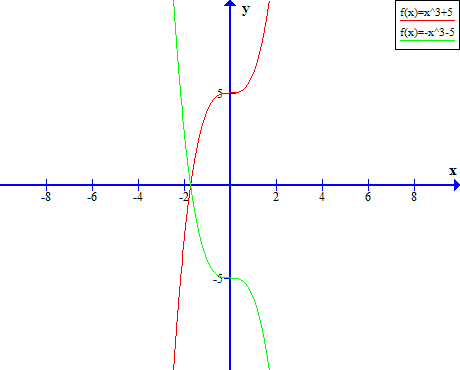
If The Graph Y X 3 5 Is Reflected In The X Axis What Is The New Equation Socratic

Solution Assume That F 2 3 Assume Also That The Graph Of Y F X Is Symmetric With Respect To The Line X 3 Find Another Value For The Function

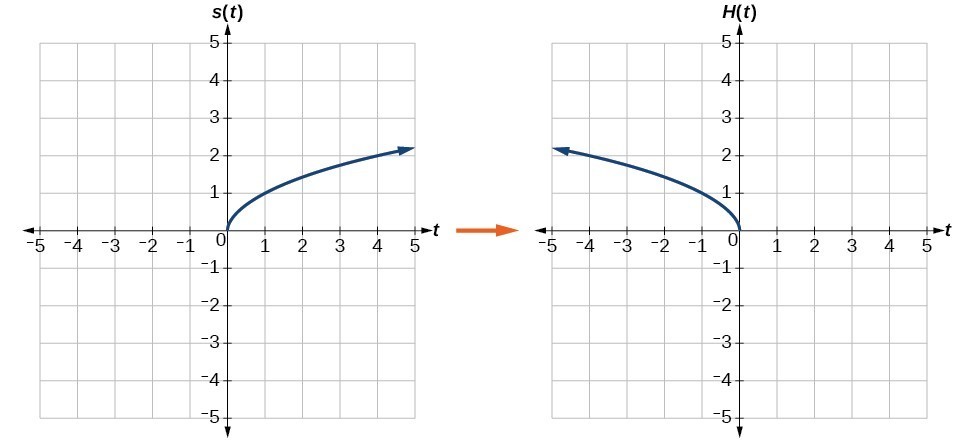
Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra

6rwjzwil Ayz8m

Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation

Which Graph Represents A Reflection Of F X 2 0 4 X Across The Y Axis Studyrankersonline

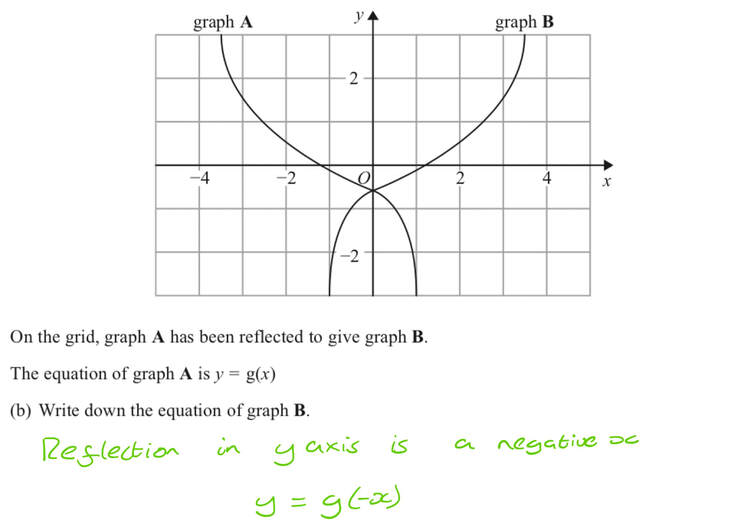
Q18 Answers Paper 1 November 18 Edexcel Gcse Maths Higher Elevise

Solved O Graphs And Functions Transforming The Graph Of A Function By Reflecting Over An Axis A The Whofy F X Is Shown Draw The Graph Of Y Course Hero

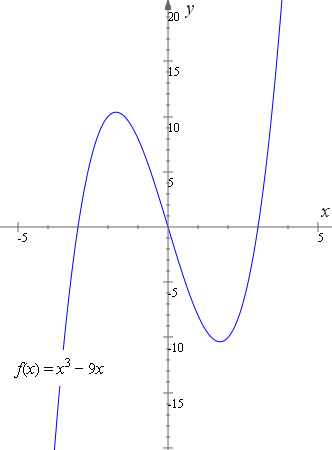
How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics

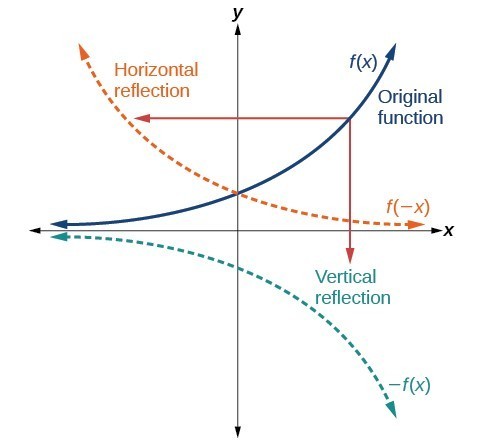
Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra

Graphing Reflections Of The Basic Rational Function F X 1 X Youtube

Worksheet 1 Abbynet

Reflecting Graphs

Biomath Transformation Of Graphs

Using Transformations To Graph Functions

Operations On Functions Reflections And Rotations Sparknotes

Simple Graph Transformation Question Rightarrow 1 F X Mathematics Stack Exchange

Graphing Shifted Functions Video Khan Academy

Transformations Of Graphs Reflections Y F X Y F X Proof Examsolutions Youtube

Graphing Reflections Y F X Or Y F X Youtube

Answered The Graph Y F X Contains The Point Bartleby

Which Graph Represents A Reflection Of F X 2 0 4 X Across The Y Axis Studyrankersonline

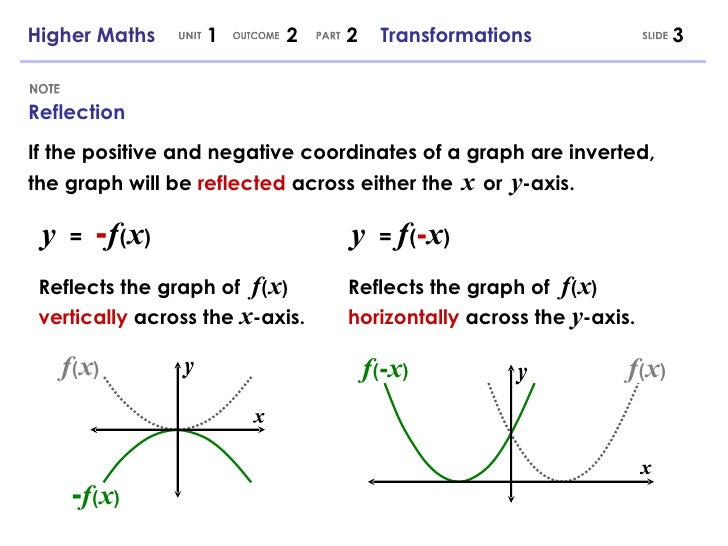
Higher Maths 1 2 2 Graphs And Transformations

How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics

How Do You Graph A Reflection Of A Function Printable Summary Virtual Nerd

Operations On Functions Reflections And Rotations Sparknotes

What Is The Difference Between Y F X And Y F X Quora

Reflect Function About Y Axis F X Expii

Transformations Of Functions Mathbitsnotebook A1 Ccss Math

Reflecting Functions Examples Video Khan Academy

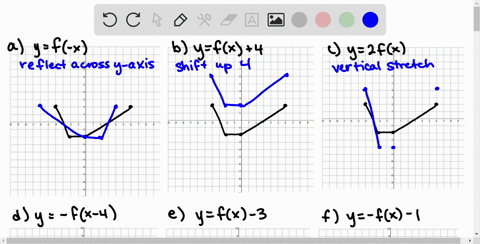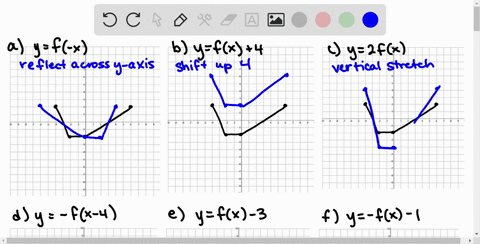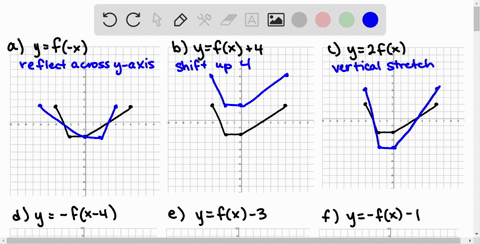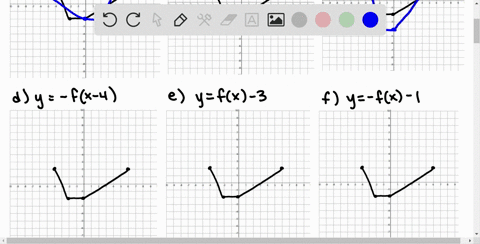
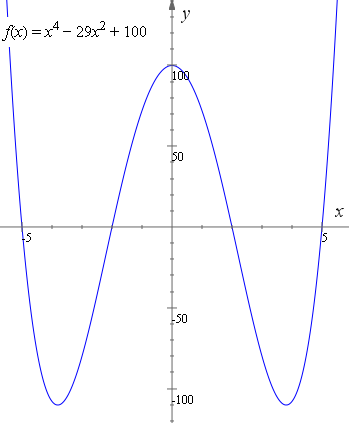
Solved Use The Graph Of F To Sketch Each Graph To Print An Enlarged Copy Of The Graph A Y F X 2 B Y F X C Y F X 2 D Y F X 3 E Y 2 F X F Y F X G Y F Left Frac 1 2

Reflecting Graphs

Operations On Functions Reflections And Rotations Sparknotes

Content Geometric Transformations Of Graphs Of Functions

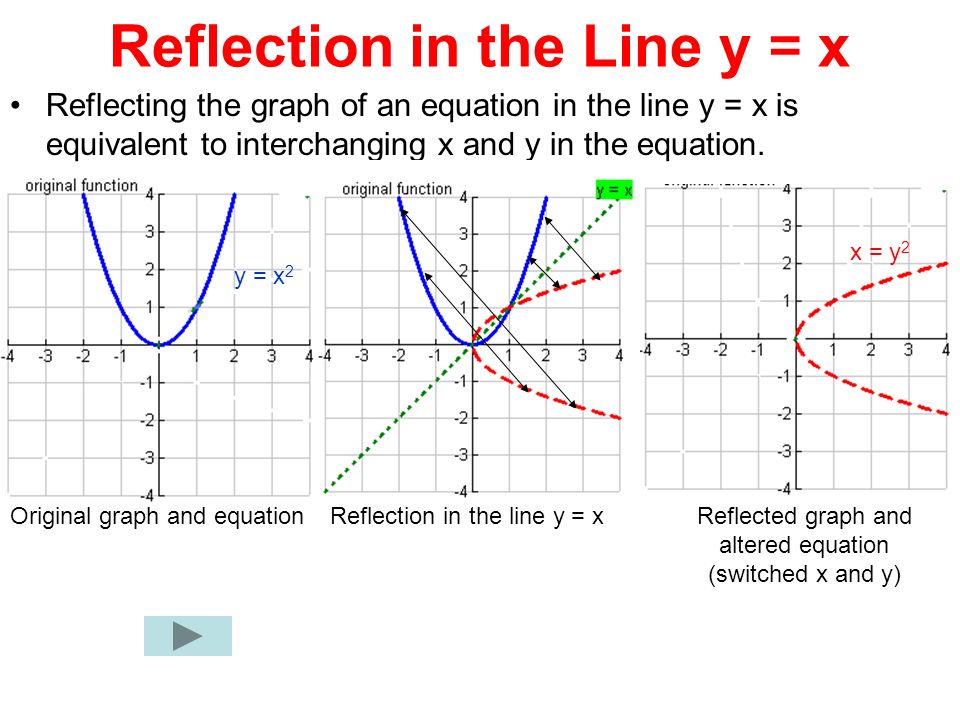
Section 4 3 Reflecting Graphs Symmetry Objective To Reflect Graphs And To Use Symmetry To Sketch Graphs Ppt Download

3 5 Transformations Of Graphs Graph Functions Using

Operations On Functions Reflections And Rotations Sparknotes

1 5 Shifting Reflecting And Stretching Graphs

A Review Of Logarithms

Using Transformations To Graph Functions

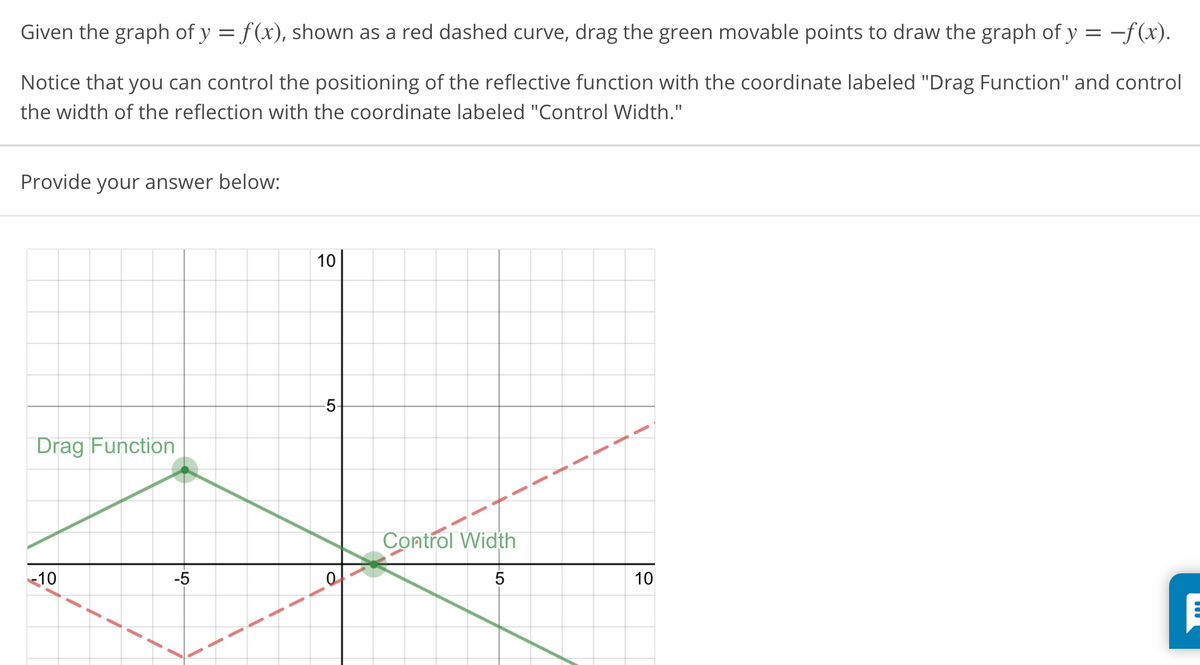
Answered Given The Graph Of Y F X Shown As A Bartleby

Reflections Of Trig Graphs Examsolutions

1

Transforming Exponential Graphs Example 2 Video Khan Academy

Question Video Combined Transformations Of Graphs Nagwa

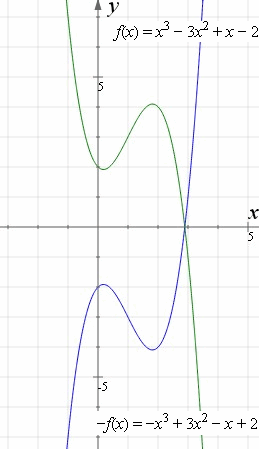
How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics

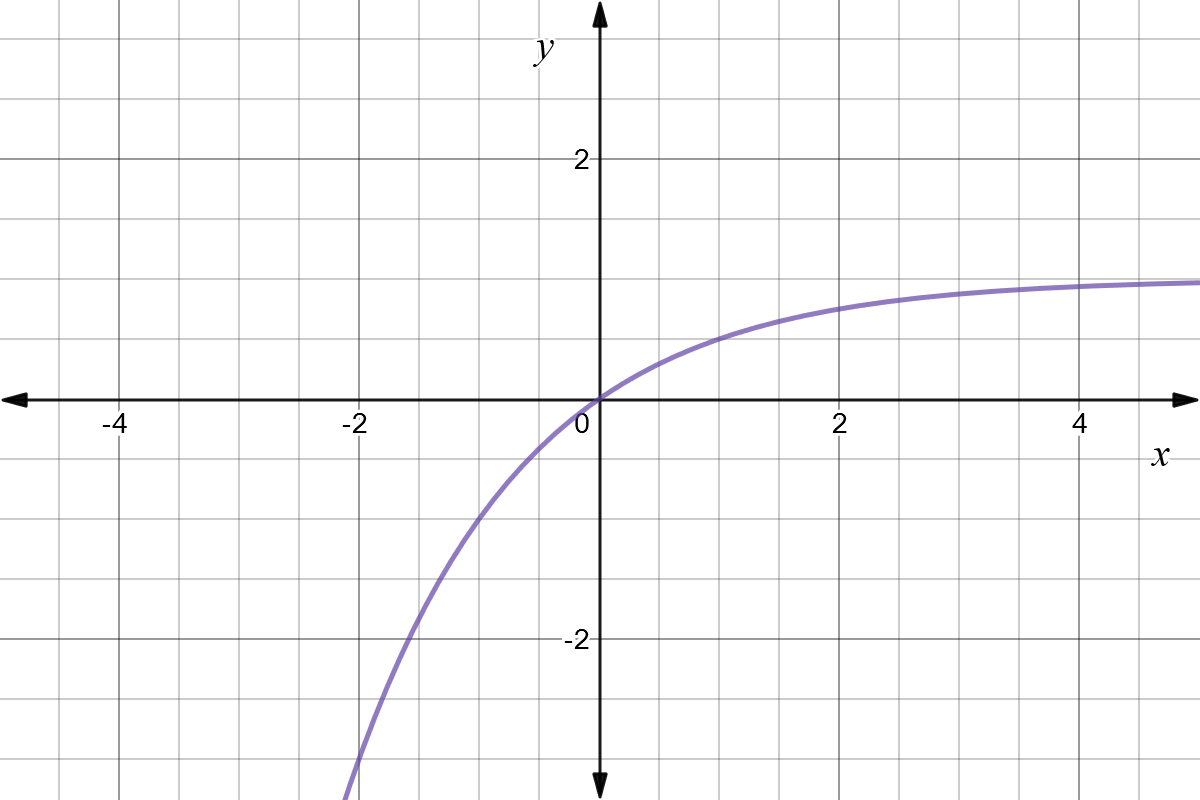
Reflect Function About Y Axis F X Expii

Warm Up Determine Whether The Graph Of Each Equation Is Symmetric Wrt The X Axis The Y Axis The Line Y X The Line Y X Or None X Axis Y Axis Ppt

Solved Starting With The Graph Of F X 3 X Write The Chegg Com

Biomath Transformation Of Graphs

Transformation Of Graphs Maths Numeracy Educational School Posters

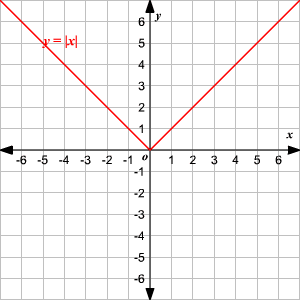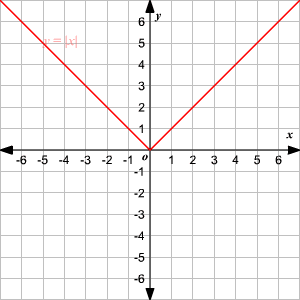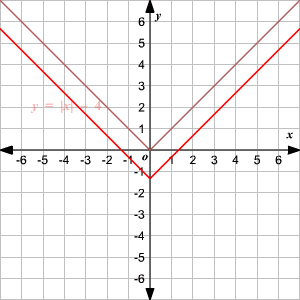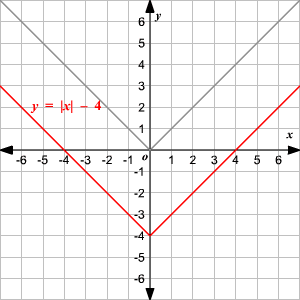
Absolute Value Functions

Write A Function G Whose Graph Represents A Reflection In The Y Axis Of The Graph Of F X 2x 1 3 Brainly Com

How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics

1

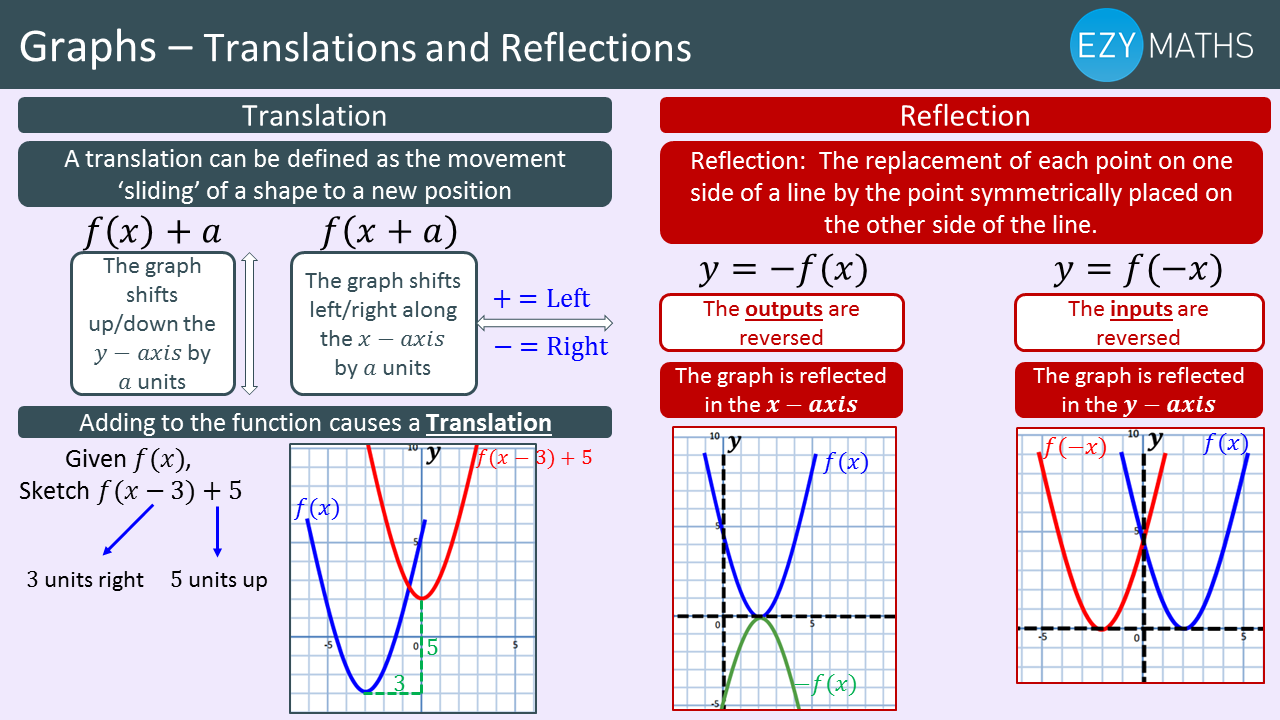
Maths Gcse Exam Revision Translations And Reflection Of Graphs Ezyeducation

Section 4 3 Reflecting Graphs Symmetry Objective To Reflect Graphs And To Use Symmetry To Sketch Graphs Ppt Download

The Graph Of F X 2x Is Shown On The Grid The Graph Of G X 1 2 X Is The Graph Of F X 2x Brainly Com

Reflections Of Graphs Examsolutions

Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation

Graphing Absolute Value Equations Dilations Reflections Video Lesson Transcript Study Com

1

Stretching Compressing Or Reflecting A Logarithmic Function College Algebra

Reflections Of A Graph Topics In Precalculus

2

Incoming Term: reflection graph y axis,